Our research topics
Medical Image Analysis
- Segmentation
- Registration
- Radiotherapy
- Radiomics
- Interpretability
Agro-environmental Modelling
- Plant growth modelling
- Crop systems biology
- Precision farming
- earth observation
Applied mathematics
- Mathematical modelling
- Statistical inference
- machine and deep learning
- Optimization, optimal control
- Stochastic process
Our research projects
Prism
Prism
funded by ANR - collaboration between Gustave Roussy, CentraleSupélec, Inserm, Université Paris-Saclay
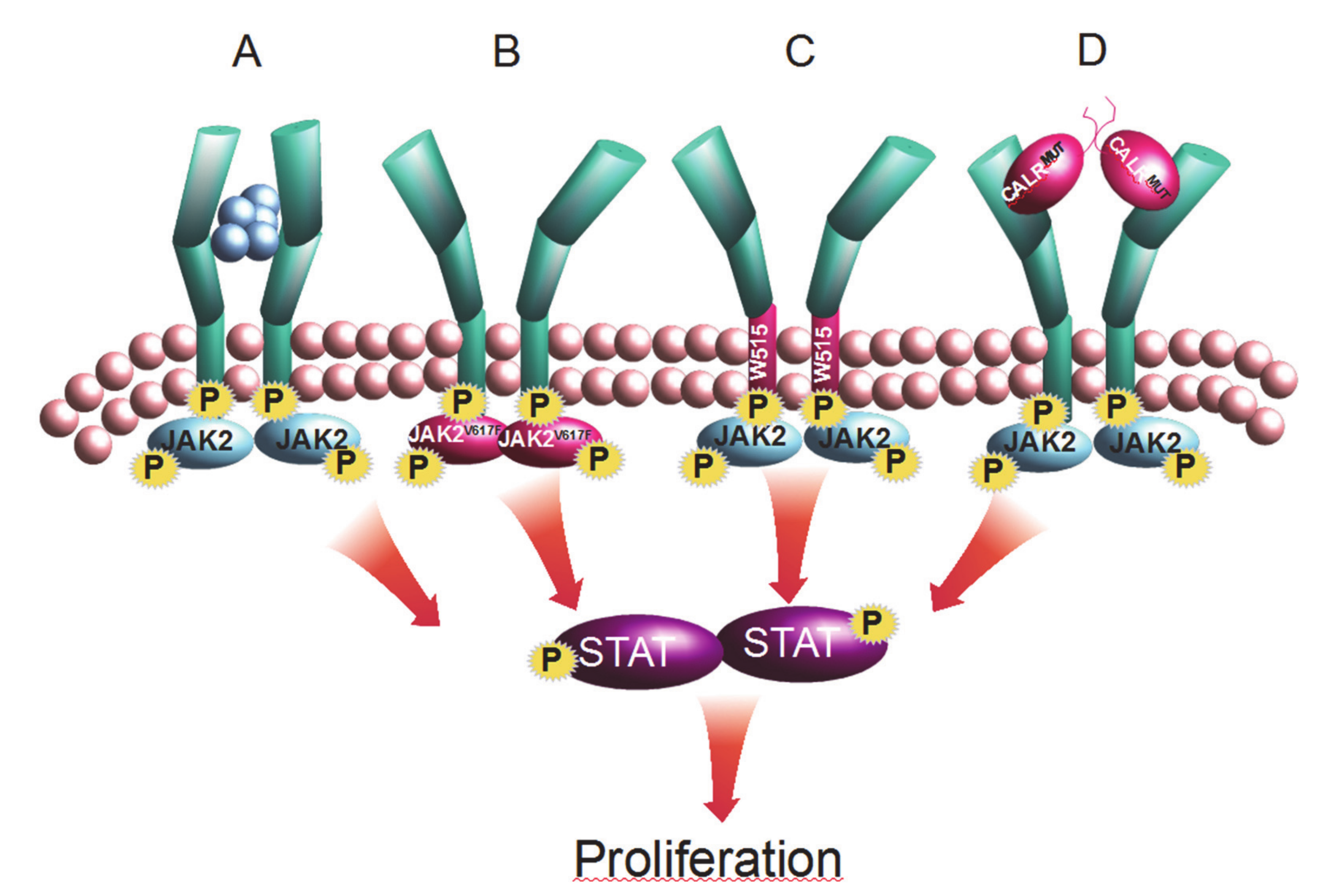
Target molecular mechanisms of cancer progression, assess biology cancer in its complexity and develop new IA methods, biotechnologies to model the early development of the disease, in order to deliver robust precision medicine tools.
OptiMyN
OptiMyN
2021 - 3 years
Collaboration with Gustave Roussy and Institut Curie
coordinator: Paul-Henry Cournède
Collaboration with Gustave Roussy and Institut Curie
coordinator: Paul-Henry Cournède
Develop mathematical models of short-term and long-term hematopoiesis in patients with blood cancers (MPN), study the impact of IFNα, and develop predictive tools for clinicians.
RadioPred Tool
RadioPred Tool
2020- 3years - INSERM
coordinator: Veronique Lefort
coordinator: Veronique Lefort
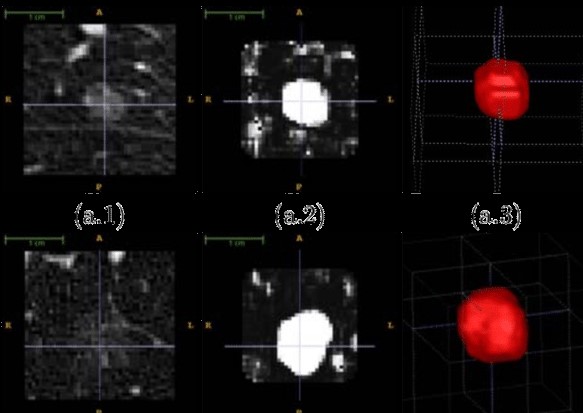
Mathematical and computational modeling approaches to set up a personalized prediction tool of late iatrogenic effects of radiotherapy using voxel-scale distribution: Application to pediatric cancers