βiomathematics
Mathematical modelling and statistical inference for biological complex systems and data
Mathematical modelling and statistical inference for biological complex systems and data
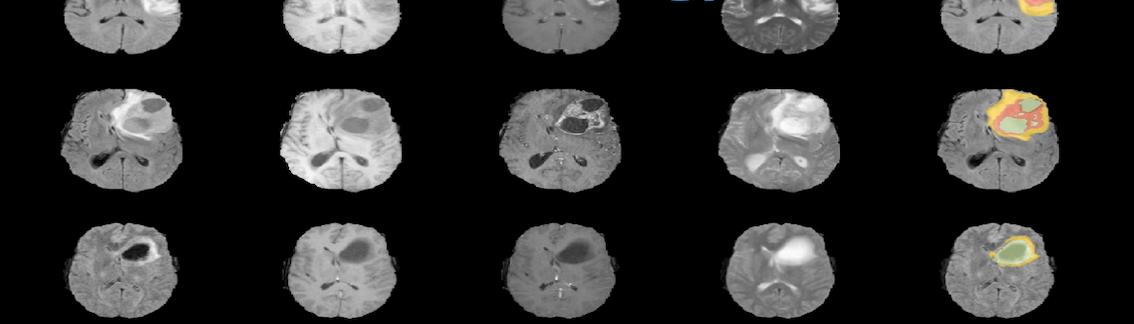
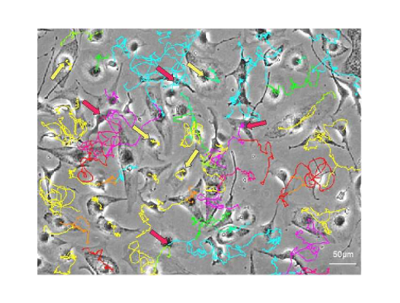
The Biomathematics team is part of the MICS (Mathematics and Informatics for Complexity and Systems) laboratory of CentraleSupelec. It is committed to the development of mathematical and computational methods to help solve major challenges in life sciences and health. New high-throughput experimental technologies (in genomics, imaging...) and structuration of data-bases offer vast opportunities for data analysis and interpretation. Moreover, large amounts of knowledge can be leveraged to understand the key biological processes and for the development of predictive tools. In this context, the Biomathematics team addresses the challenges of data-driven and knowledge-based mathematical and computational modeling in the biosciences.
Our research topics
Medical Image Analysis
- Segmentation
- Registration
- Radiotherapy
- Radiomics
- Interpretability
Agro-environmental Modelling
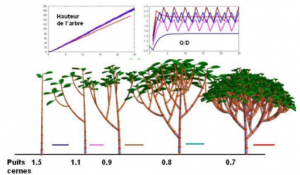
- Plant growth modelling
- Crop systems biology
- Precision farming
- earth observation
Applied mathematics
- Mathematical modelling
- Statistical inference
- machine and deep learning
- Optimization, optimal control
- Stochastic process
Events